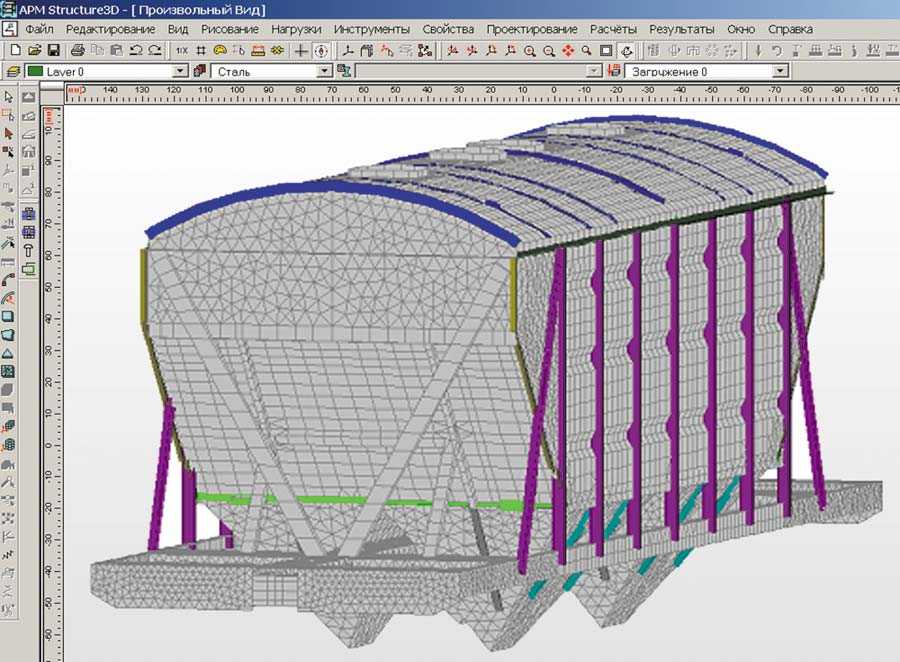
Прочностной расчет конструкций

Прочностной расчет конструкций: основные факторы и способы проведения

Прежде всего, начнем статью с определения того, что такое прочностной расчет конструкций и объяснений, зачем он нужен для Вашего производства. 

Под этим термином подразумевается начальный этап проектирования конструкции, благодаря которому можно определить действующие на нее внешние силы.

Зачем это необходимо сделать перед постройкой той или иной конструкции? Чтобы подобрать материалы и размеры элементов, которые будут хорошо выдерживать нагрузки во время эксплуатации. Это поможет продлить время работоспособности конструкции или постройки, а также получить сертификаты, подтверждающие определенный срок эксплуатации.

РАСЧЕТЫ СТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ

КЛИМАТОЛОГИЯ	СБОР НАГРУЗОК	РАСЧЕТ ОСНОВАНИЙ	РАСЧЕТ ФУНДАМЕНТОВ
СП 131.13330.2012	СП 20.13330.2016	СП 22.13330.2011	СП 50-101-2004
⇒   Районирование	⇒  Интерполяция	⇒   Расчет геологических скважин	⇒   Объем  инженерно-геологических изысканий для свайных фундаментов
⇒   Карта 1. Снег	⇒  Снеговая нагрузка СП 20.13330.2016	⇒   Расчет траншей	⇒   Расчет на всплытие подземных емкостей
⇒   Карта 2. Ветер (давление)	⇒  Ветровая нагрузка СП 20.13330.2016	⇒   Расчет котлована	⇒   Расчет глубины фундамента
⇒   Карта 3. Гололед	⇒  Распределенные нагрузки	⇒   Расчет шпунтового ограждения	⇒   Расчет сил морозного пучения
⇒   Карта 4. Минимальная температура	⇒  Сосредоточенные нагрузки	⇒   Расчет сопротивления грунта	⇒   Расчет фундаментных болтов
⇒   Карта 5. Максимальная температура	⇒  Сейсмические нагрузки	⇒   Характеристики крупнообломочных грунтов	⇒  Расчетные сопротивления под нижним концом свай
⇒   Карты сейсмических районов	⇒  Температурные нагрузки	⇒   Характеристики песчаных грунтов	⇒  Расчетные сопротивления на боковой поверхности свай
⇒   Карта глубины промерзания	⇒  Сбор нагрузок	⇒   Характеристики пылевато-глинистых грунтов	⇒  Коэффициенты условий работы грунта при расчете свай
⇒  Климатические параметры	⇒  — на фундамент	⇒   Характеристики просадочных грунтов	⇒  Предельные деформации основания фундаментов
⇒  Климатические параметры холодного периода	⇒  — на прогоны	⇒   Характеристики насыпных грунтов
⇒  Климатические параметры теплого периода	⇒  — на балки
⇒  Средняя месячная и годовая температура воздуха	⇒  — на фермы
⇒  Максимальная суточная амплитуда температуры воздуха в июле	⇒  — на колонну
⇒  Среднее месячное и годовое парциальное давление водяного пара	⇒  — на колонну (две ветви)
⇒  Суммарная солнечная радиация (прямая и рассеянная)	⇒  — на стену (наружную)
	⇒  — на лестницу
		⇒  КНИГИ ПО РАСЧЕТУ ГРУНТОВ	⇒  КНИГИ ПО РАСЧЕТУ ФУНДАМЕНТОВ

Расчет вертикального импоста по методу предельных состояний 2-ой группы

Вертикальный импостный профиль окна выбирается по требуемому моменту инерции сечения в направлении действия внешних сил.
Основной параметр расчета на деформацию и гибкость – геометрическая характеристика элемента — момент сопротивления, I см4.
Требуемый момент инерции профиля определяется для 3-х расчётных случаев.
Для простоты расчёта во всех трёх случаях принята схема закрепления стойки как шарнирно-опёртой однопролётной балки.

Момент инерции профиля должен удовлетворять условию:

Iкат – момент инерции профиля по каталогу;

Iрасч – требуемый расчётный момент инерции профиля.

Расчетный момент инерции профиля определяется по зависимости:

Iрасч= max {I1; I2; I3}, (2)

где I1; I2; I3 – расчётные моменты инерции по первому, второму и третьему расчётным случаям соответственно.

6. Расчет вертикального импоста на деформацию от ветровой нагрузки.

Расчет вертикального импоста в зависимости от ветровой нагрузки проводится по условию жесткости (1-ый расчетный случай). Применяется для всех вертикальных импостов.
Критерий расчёта – обеспечение фактического прогиба импоста меньше допускаемого.
В качестве внешнего воздействия на конструкцию принимается нормативное значение средней составляющей ветровой нагрузки по СНиП 2.01.07-85*.
Расчётная схема приведена на рис. 1.

Рис. 1.

Условие работоспособности по данному критерию может быть записано в виде:

fфакт — фактический прогиб импоста от действия внешней нагрузки, который может быть определён по формуле:

q – распределённая нагрузка на импост от действия нормативной ветровой нагрузки;

Е – модуль упругости алюминия, принимаемый по таблице 3 обязательного приложения 1
CНиП 2.03.06-85 в зависимости от температуры эксплуатации.

При температуре эксплуатации от –40 до +50С модуль упругости Е = 0,71•106 кгс/см2.

fдоп — допускаемый прогиб импоста, определяемый по таблице 42 CНиП 2.03.06-85, и равный:

В случае остекления одним стеклопакетом по всей высоте вертикального импоста, допускаемый прогиб импоста должен быть не более 8 мм.

Приравнивая в неравенстве (3) фактический прогиб к допускаемому прогибу, и используя соотношения (4), (5) получаем формулу для определения расчётного момента инерции импоста при одинарном остеклении:

Аналогично получаем формулу для определения расчётного момента инерции импоста при остеклении стеклопакетами:

Распределённая нагрузка на импост при известном шаге определяется по формуле:

Jf =1,0 – коэффициент надёжности по нагрузке, принятый в соответствии с п. 1.3 СНиП 2.01.07-85* «Нагрузки и воздействия»;

Wm – нормативное значение средней составляющей ветровой нагрузки, определяемое по СНиП 2.01.07-85* «Нагрузки и воздействия»; формула (6).

W0 – нормативное значение ветрового давления, принимается по таблице 5 СНиП 2.01.07-85* в зависимости от принадлежности объекта к ветровому району;

с=0,8 – аэродинамический коэффициент для фронтальной конструкции;

с=2,0 – аэродинамический коэффициент для угловой конструкции;

k – коэффициент, учитывающий изменение ветрового давления по высоте, по таблице 6 СНиП 2.01.07-85*, в зависимости от типа местности и высоты витража над поверхностью земли;

10-4 – коэффициент перевода wm из [кгс/м2 ] в [кгс/см2].

Согласно СНиП 2.01.07-85* «Нагрузки и воздействия» ветровую нагрузку следует определять как сумму средней и пульсационной составляющих.

Wр —нормативное значение пульсационной составляющей ветровой нагрузки определяемое по формуле 8 СНиП 2.01.07-85.

ζ — коэффициент пульсаций давления ветра, принимаемый по табл. 7 СНиП 2.01.07-85 в зависимости от высоты и типа местности.

ν — коэффициент пространственной корреляции пульсаций давления ветра, определяемый по таблице 9 СНиП 2.01.07-85 в зависимости от размеров расчётной поверхности.

При этом в расчетах многоэтажных зданий высотой до 40 м и одноэтажных производственных зданий высотой до 36 м при отношении высоты к пролету менее 1,5, размещаемых в местностях типов А и В (см. п.6.5 СНиП2.01.07-85), пульсационную составляющую ветровой нагрузки допускается не учитывать.

В них присутствуют следующие расчеты:

расчет импоста по условию гибкости;

расчет импоста на деформацию от сосредоточенной нагрузки;

расчет горизонтального импоста по методу предельных состояний 1-ой группы;

расчет прочности импоста от ветровой нагрузки;

расчет прочности импоста от нагрузки стеклом;

расчет горизонтального импоста по методу предельных состояний 2-ой группы;

расчет импоста на деформацию от ветровой нагрузки;

расчет импоста на деформацию от нагрузки стеклом;

расчет на деформацию от сосредоточенной нагрузки.

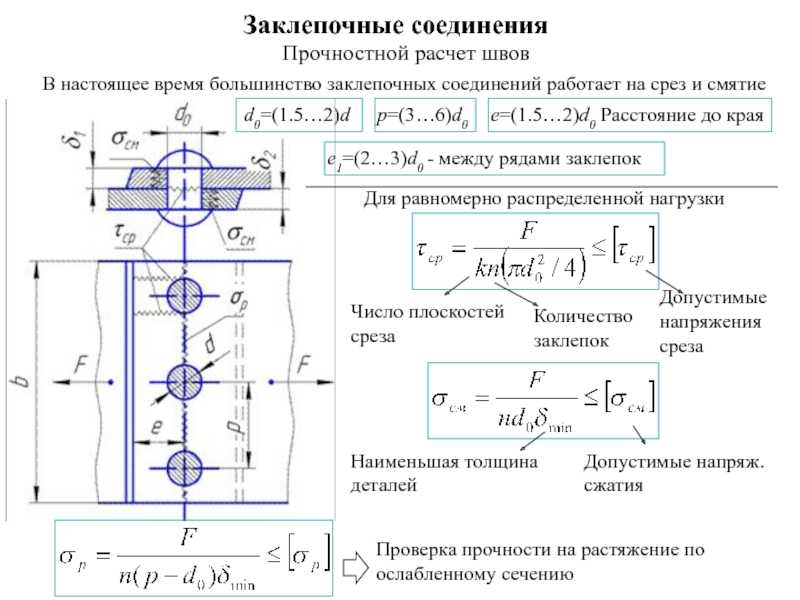
Коэффициент прочности шва

Это показатель φ, являющийся отношением между собой прочностей сварной дорожки и основного материала. Его значение нормировано и определяется способом сварки и конструкцией стыка. Он принимается на основании Правил Госгортехнадзора и отражается в приложениях ГОСТов Р52857.1-2007, 14249-89 и 34233.1-2017.

Таблица 1. Коэффициенты прочности сварочных швов

Тип сварного соединения	Значение φ
Контролируемый участок от общей протяженности шва:
100%	10-50 %
Стыковое одностороннее, выполненное ручной сваркой	0,9	0,65
Тавровое, с конструктивно предусмотренным зазором между деталями	0,8	0,65
Встык одностороннее, производимое с подкладкой из флюса или керамики, автоматической или полуавтоматической сваркой	0,9	0,8
Втавр или встык со сплошным двусторонним проваром, выполняемый автоматикой или полуавтоматикой	1,0	0,9
Стыковое с подвариванием корня шва или тавровый со сплошным проваром с 2 сторон, выполненные ручной сваркой	1,0	0,9
Одностороннее встык, во время сварки имеет со стороны корня шва металлическую подкладку, прилегающую к основному материалу по всей длине шва	0,9	0,8

Коэффициент прочности для дорожек, паянных мягкими и твердыми припоями с использованием аппаратов из цветных металлов, составляет 0,7 для композиционной пайки, 1 — для однородной.

Зависимость от типа сварочного шва

Существует несколько вариантов сцепления металлических элементов в единую конструкцию. По расположению соединяемых деталей различают следующие виды сварных швов:

1. Стыковой — наиболее рациональный, т. к. концентрация напряжения в шве при таком методе минимальна. Свариваются торцы деталей, в результате одна часть изделия продолжает другую.
2. Угловой — соединяемые элементы располагаются перпендикулярно друг другу. Прочность здесь во многом зависит от верно рассчитанного предельного усилия.
3. Тавровый — похож на угловой с той лишь разницей, что детали свариваются торцами. Такая дорожка прочная, экономичная и простая в выполнении.
4. Нахлесточный — края сцепляемых деталей несколько находят друг на друга. Такой тип позволяет укрепить соединение и применяется там, где нужно сварить металл толщиной не более 5 мм.

Прежде чем начинать вычисление прочности будущего сцепления, нужно рассчитать площадь его поперечного сечения. Для этого длину сварного соединения умножают на его толщину.

Соединение листов внахлест

Для расчета напряжения среза используют формулу:

где:

• P — нагрузка на шов, Н;
• ’ср — допускаемое напряжение на срез, Па;
• 0,7k — толщина шва в наиболее опасном сечении, см;
• l — длина сварной дорожки, мм.

При соединении внахлест разделка кромок не требуется.

Значение нагрузки P таково:

При расчете учитывают минимальную площадь сечения сварной дорожки в поперечнике. Это связано с тем, что сварочные материалы по прочности могут превышать основной металл.

Угловые конструкции

Такие соединения рассчитываются на основании их поперечного сечения, причем наименьшего, т. е. в наиболее опасном месте дорожки. Показатель устойчивости простого углового шва на изгиб, когда он нагружен лишь моментом M, вычисляется так:

где:

• Wc — момент сопротивления опасного сечения дорожки (шва);
• M — изгибающий момент.

Угловые конструкции рассчитываются на основании их поперечного сечения.

А напряжение простого углового соединения на срез запишется таким образом:

где:

• M — нагружающий момент на срез;
• Fc = 0,7kl — площадь сечения дорожки в опасном месте, мм²;
• P — допустимая нагрузка на дорожку.

При расчете угловых сварных швов на срез применяется общепринятое выражение:

где:

• N — максимальная нагрузка, давящая на линию сцепления;
• с — коэффициент условий рабочей среды, значение указано в стандартизированных таблицах;
• ßf, ßz — постоянные величины, не зависящие от марки металла, ßz = 1, ßf = 0,7;
• Rwf — сопротивление срезу, табличная величина для разных материалов;
• Rwz — сопротивление на линии стыка; стандартные, постоянные табличные величины;
• kf — толщина дорожки, измеряется по линии сплавления;
• Ywf — для стыка материала с сопротивлением 4200 кгс/см² составляет 0,85;
• Ywz — 0,85 для всех марок стали;
• lw — общая длина стыка, уменьшенная на 10 мм.

В определении длины сварочного сцепления на отрыв обязательно учитывают силу, направленную к центру тяжести. При этом площадь сечения выбирают в самом опасном месте дорожки, т. е. наименьшую.

Тавровые швы

Условие прочности сцепления втавр, выполненного встык и работающего на растяжение Р и момент M, выглядит так:

Формула для такого же, но не стыкового, а углового шва:

Тавровые швы могут быть односторонними и двусторонними.

Если тавровое соединение будет нагружено изгибом и крутящим моментом, то применяется уравнение:

Крутящая и изгибающая сила соответственно определяются следующими формулами:

и

Сварка на стыке

Расчет шва встык, который будет работать на сжатие либо на растяжение, выполняется по уравнению:

где:

• l — длина сварочной дорожки, мм;
• P — нагрузка, действующая на стык, Н;
• s — толщина соединяемых деталей, мм;
• ’ р1сж1 — допускаемое для сцепления напряжение на растяжение либо сжатие, Па.

Допустимая действующая нагрузка P составит:

Стыковое сцепление, работающее на изгиб, рассчитывается по формуле:

где:

• М — это изгибающий момент, Н/мм;
• Wc — момент сопротивления расчетного сечения.

Если напряжение шва возникает и от изгиба М, и от сжатия либо растяжения Р, то оно определяется уравнением:

Построение эпюр для консольной балки

В качестве первого примера, возьмём консольную балку, жёстко закреплённую с левого торца и загруженной следующим образом:

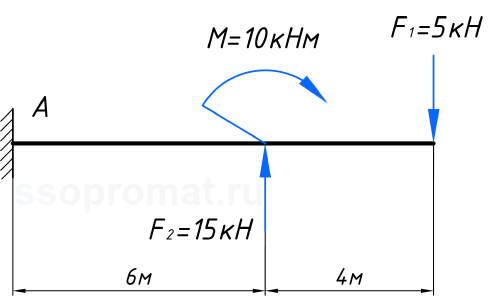
Будем рассчитывать балку справа налево.

Рассмотрим первый участок

Обозначим некоторое сечение 1-1 на расстоянии x₁, от свободного торца балки, при этом x₁ будет находиться в диапазоне: 0 ≤ x₁ ≤ 4м.

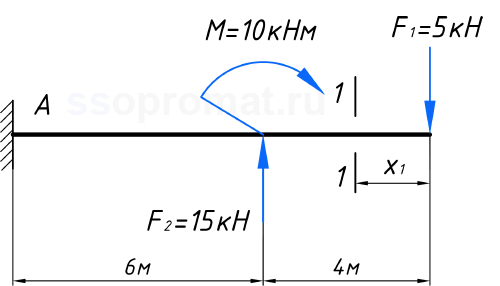
Так как расчёт выполняется справа налево, то в уравнениях необходимо учесть всю нагрузку, которая находится правее рассматриваемого сечения. Как видишь, на этом участке действует всего лишь одна сила F. Её и будем учитывать.

Поперечные силы на первом участке

Сила F, относительно сечения 1-1, поворачивает ПО часовой стрелке, поэтому , записываем её с «плюсом»:

Как видишь, поперечная сила будет постоянна на первом участке:

Уже можем отразить это на эпюре поперечных сил:

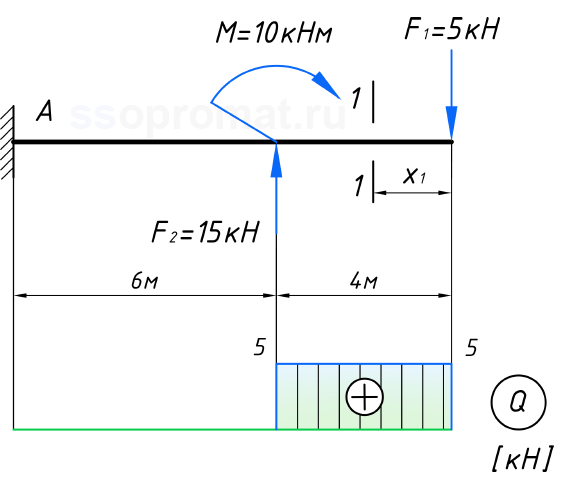
Изгибающие моменты на первом участке

Теперь запишем уравнение для изгибающих моментов. Сила F растягивает верхние волокна, поэтому , нужно учесть момент силы F со знаком «минус»:

Здесь уже изгибающие моменты будут меняться по линейному закону. , чтобы построить эпюру изгибающих моментов на участке, нужно вычислить значения на границах участка:

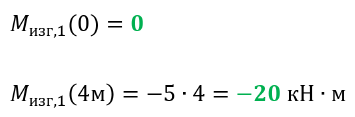
Откладываем полученные значения:

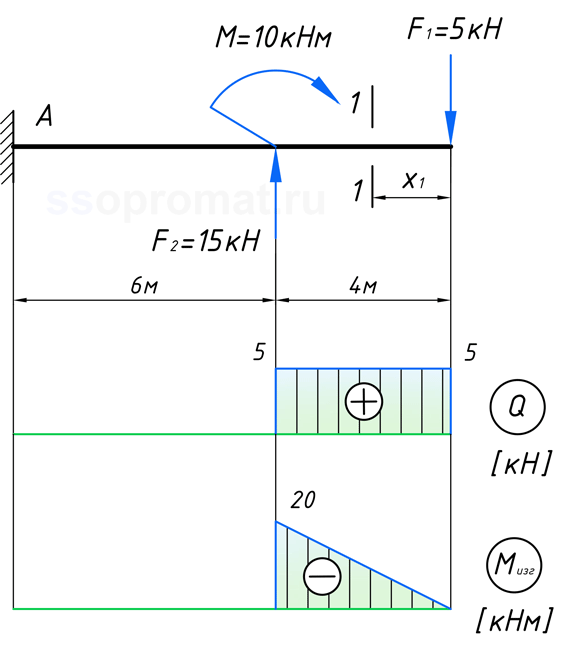
Расчёт второго участка

Переходим ко второму участку. Также будем рассматривать некоторое сечение 2-2, на расстоянии x₂ от начала участка (0 ≤ x₂ ≤ 6м). Здесь также нужно учесть ВСЮ нагрузку, которая находится справа от сечения 2-2.

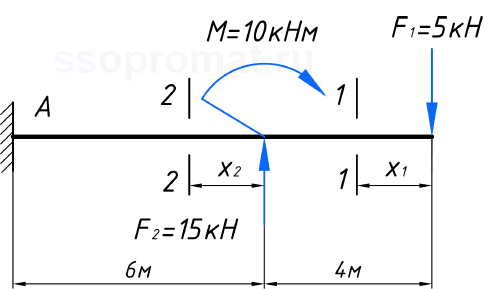
Поперечные силы на втором участке

Теперь на участке будут действовать 2 силы (сосредоточенный момент — M, никак не влияет на эпюру поперечных сил), учитываем их с учётом :

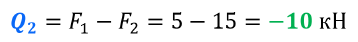
Теперь можем показать окончательную эпюру поперечных сил:

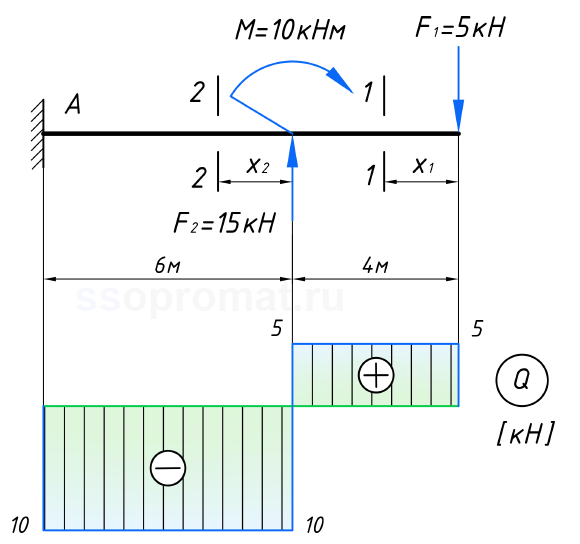
Изгибающие моменты на втором участке

Для изгибающих моментов, с учётом , второе уравнение будет выглядеть следующим образом:

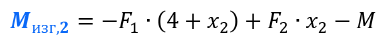
Вычисляем значения на границах второго участка:

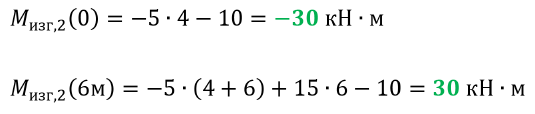
Показываем окончательную эпюру изгибащих моментов:

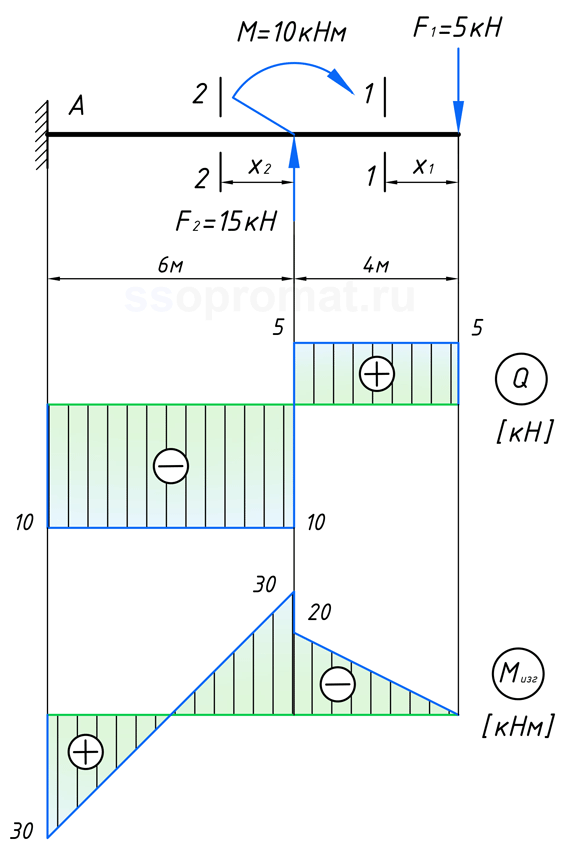
Проверка построенных эпюр

Балку можно рассчитать и слева направо. При этом очевидно, должны получаться те же эпюры. Давай проверим себя и рассчитаем эту балку с другой стороны.

Первым делом, нам потребуется определить реакции в заделке:

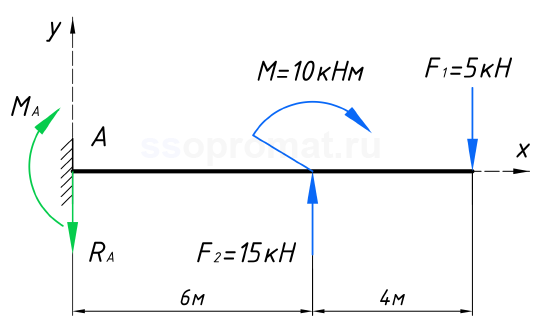
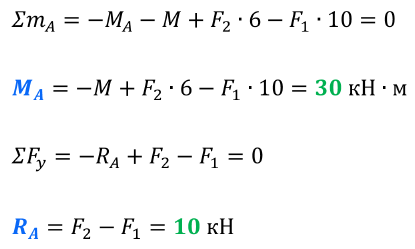
Расчёт эпюр поперечных сил и изгибающих моментов

Рассчитываем все участки теперь слева направо:

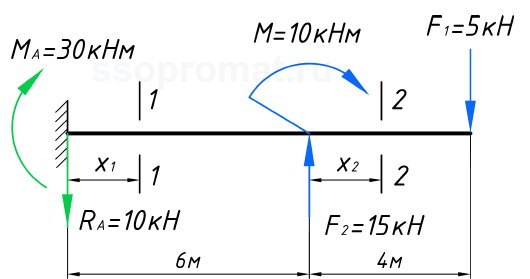
Ожидаемо, получили те же эпюры поперечных сил и изгибающих моментов:

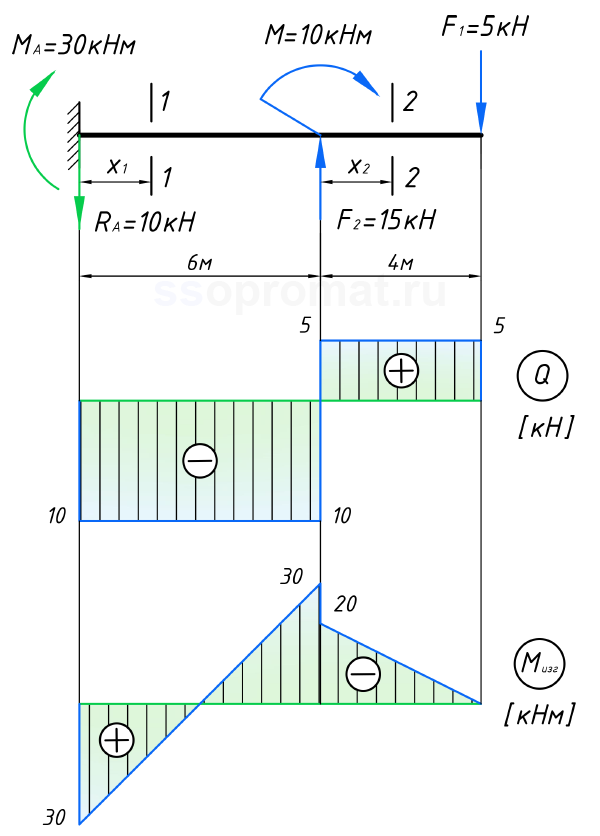
Причём не обязательно считать все участки балки только слева направо или справа налево. Можно считать балку с разных сторон:

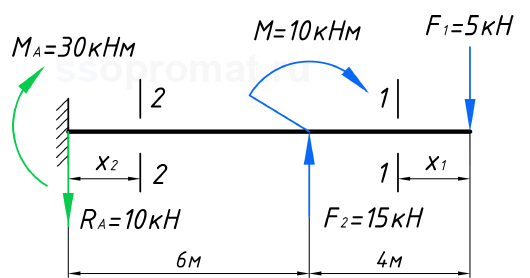
Такой подход позволяет минимизировать расчёт: когда балка имеет много расчётных участков. Как раз так и будем считать вторую .

Эпюра моментов со стороны растянутых или сжатых волокон

По построенной эпюре можно явно сказать, какие волокна балки будут растянуты, а какие сжаты. Это очень полезная информация, при проведении прочностных расчётов.

Причем сама эпюра была построенна со стороны растянутых волокон:

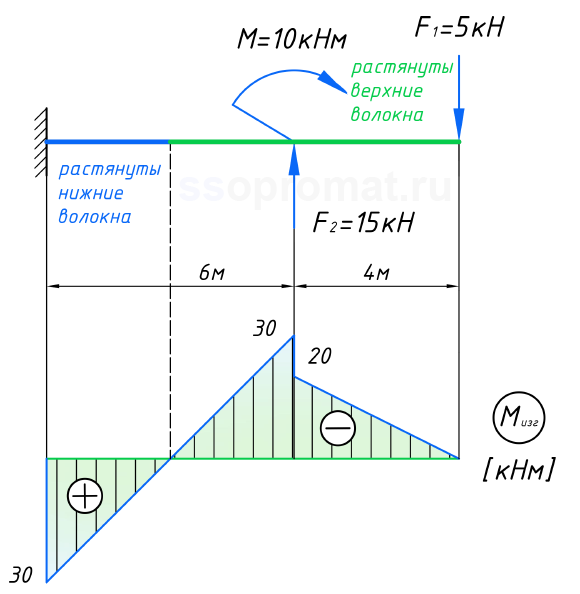
Однако, студентов некоторых специальностей учат строить эпюры, с другой стороны – со стороны сжатых волокон:

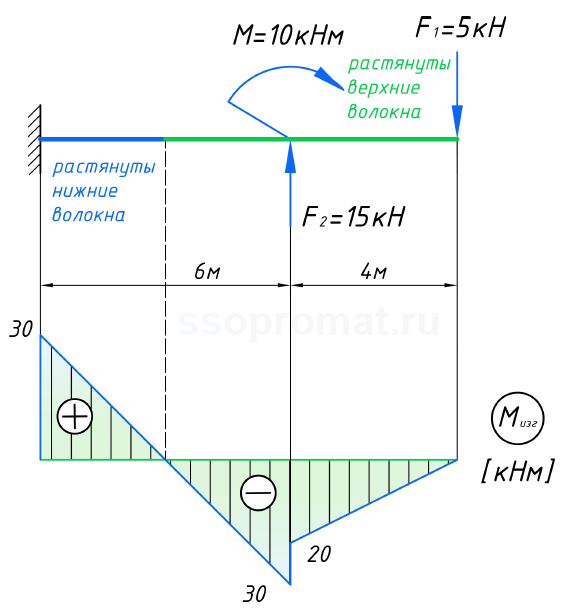
Как видишь, в первом случае, отрицательные значения на эпюре моментов откладываются выше нулевой линии, а во втором – ниже. При этом для расчета эпюр и сами расчёты не меняются. Обычно эпюры «на растянутых волокнах» строят студенты — строители, а эпюры «на сжатых волокнах» строятся студентами машиностроительных специальностей. В конечном счёте с какой стороны ты будешь строить эпюры, будет зависеть от твоего преподавателя, как он учит. В своих уроках я буду строить эпюры моментов со стороны растянутых волокон.

Какие параметры используются в расчете

В расчете на прочность сварных соединений необходим целый ряд показателей.

Их знание позволяет провести подсчеты с наименьшей погрешностью.

При этом учитывают следующие основные параметры:

• Ry — сопротивление материала изделия с учетом предела текучести; это постоянная величина для каждого металла;
• Ru — сопротивление материала в соответствии с временным сопротивлением; стандартный табличный показатель;
• Rwy — сопротивление с учетом предела текучести;
• N — предельно допустимая нагрузка, которую может выдержать сцепление;
• t — минимальная толщина соединяемых деталей;
• lw — максимальная длина сварного стыка, при вычислении ее уменьшают на 2t;
• gс — коэффициент условий, которые преобладают на рабочем месте; стандартизированный параметр, присутствует в общепринятых таблицах, в частности, в методичках для сварщиков.

Процесс растяжения и сжатия металла вычисляют по формуле:

Если при изготовлении изделия свариваются детали из разных металлов, то в формулах используются Ry и Ru для материала с наименьшей прочностью. Аналогично поступают при включении параметров в расчете шва на срез.

При расчете на прочность необходим ряд показателей.

Кроме названных числовых показателей на надежность соединения влияют:

• качество материала изделия;
• правильно подобранные расходные материалы (присадки, электроды);
• режим сварки, в т. ч. полярность и сила тока;
• тщательность обработки заготовок — на кромке стыков не должно быть никаких деформаций и посторонних вкраплений;
• соответствие сварного аппарата требуемой технологии сварки и мощности.

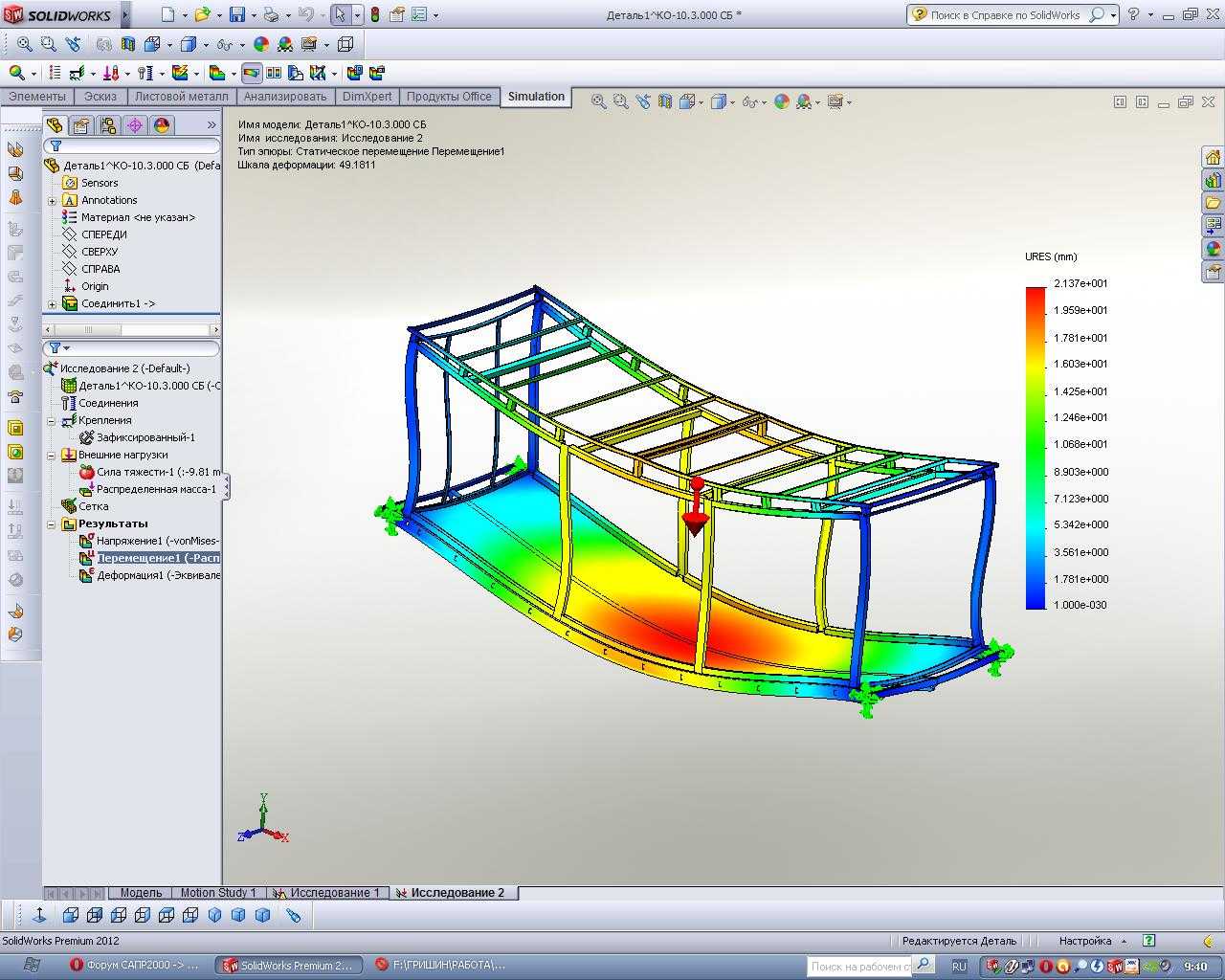
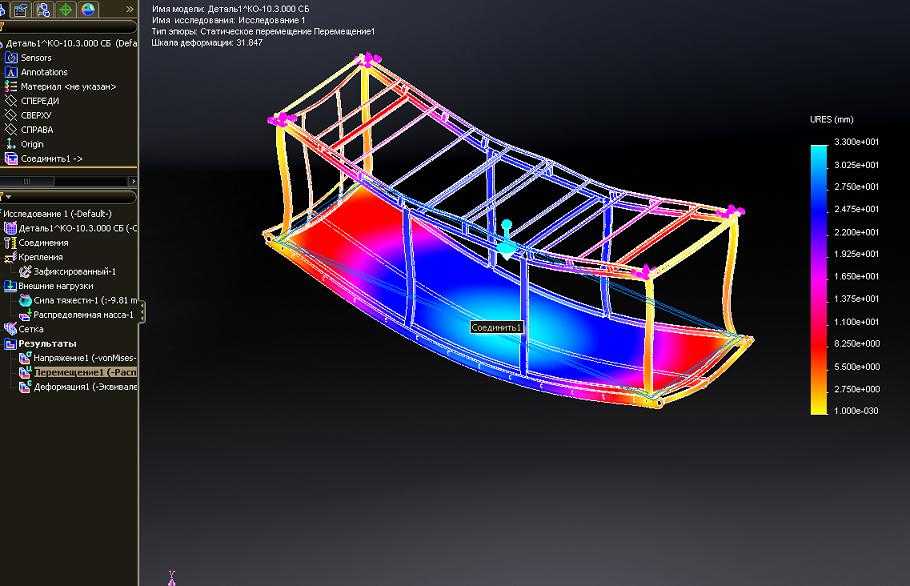
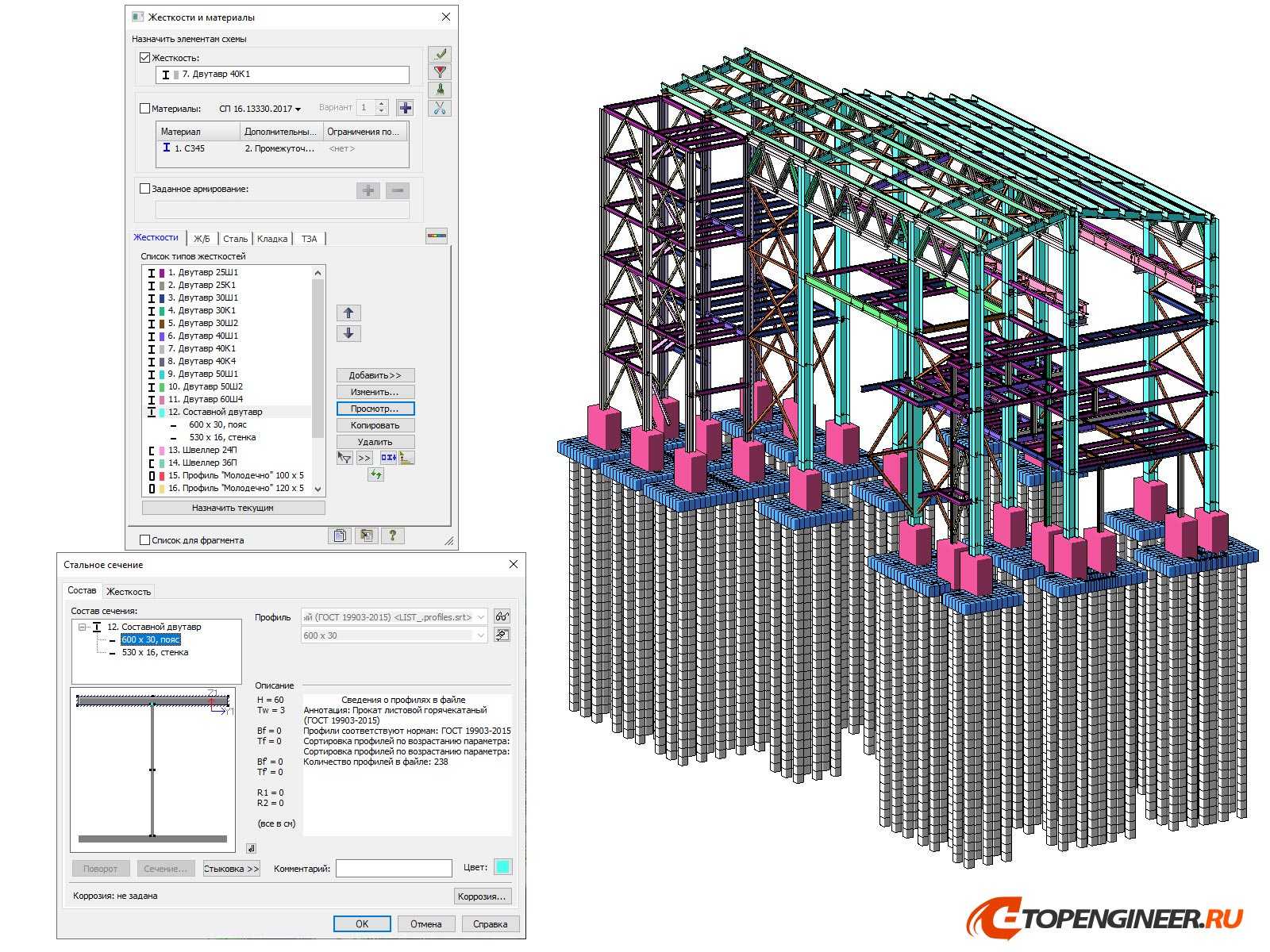
Возможности программного продукта для прочностного расчета конструкций

Существует много различных возможностей в разных плоскостях расчета. Рассмотрим их по группам:

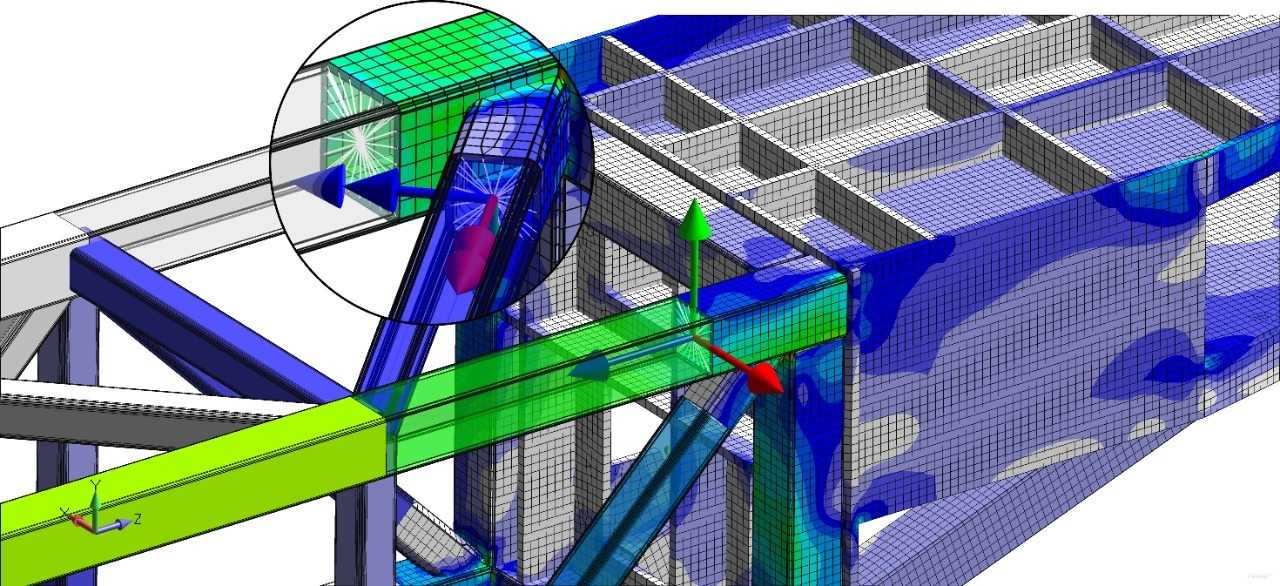
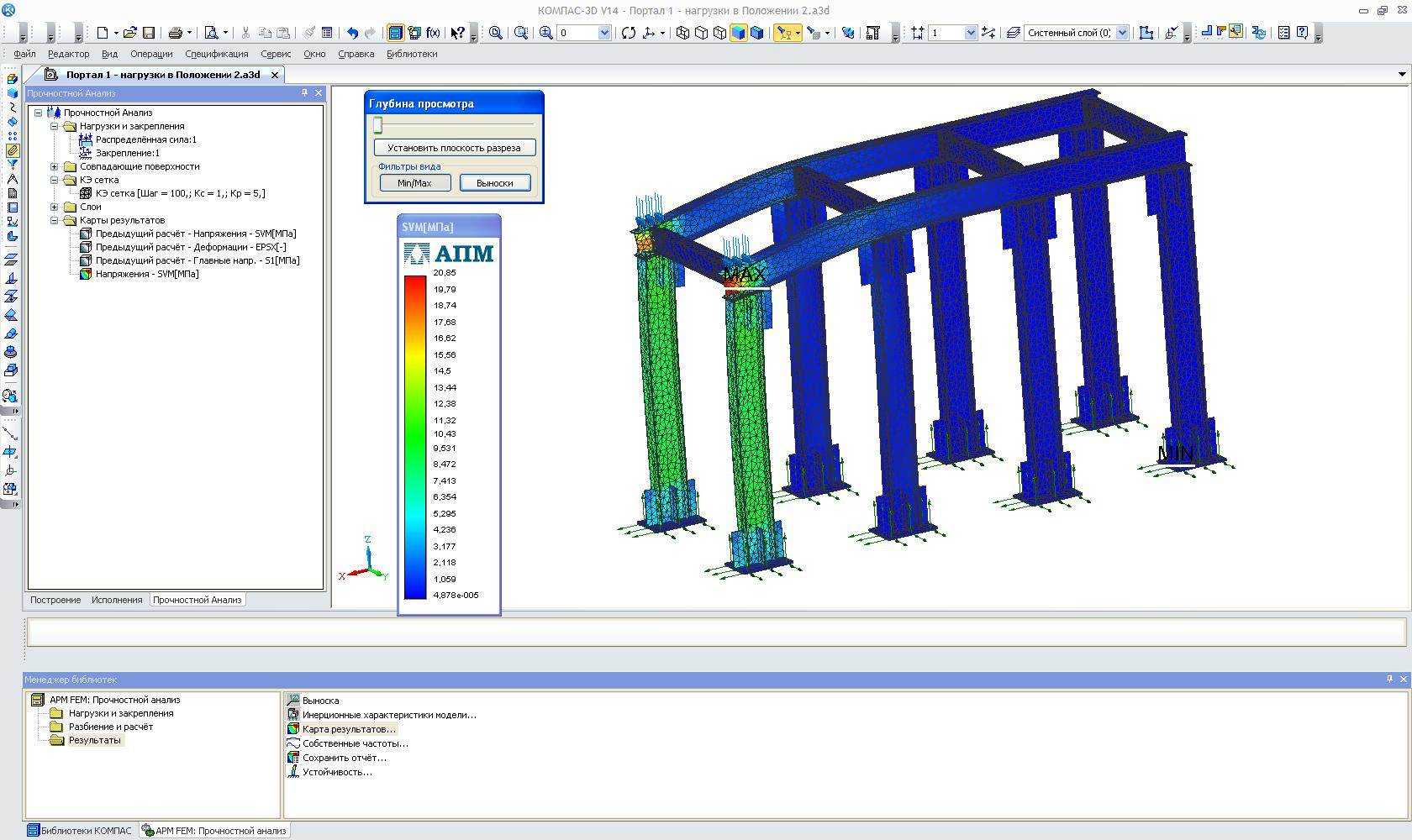
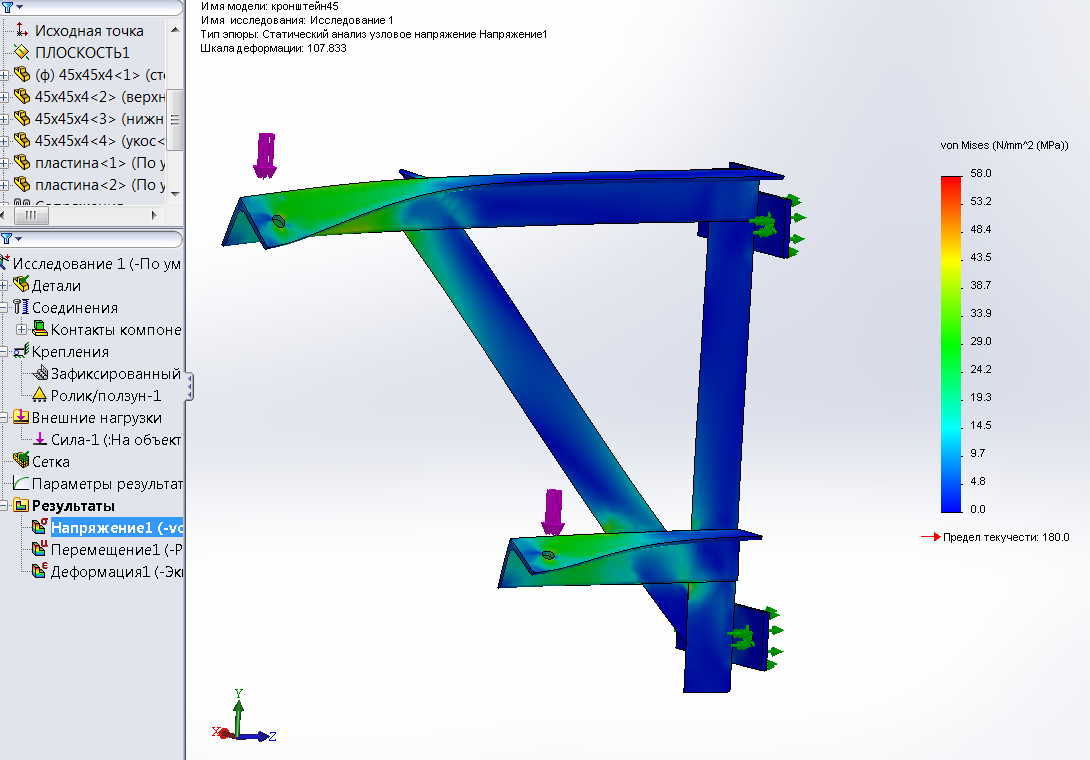
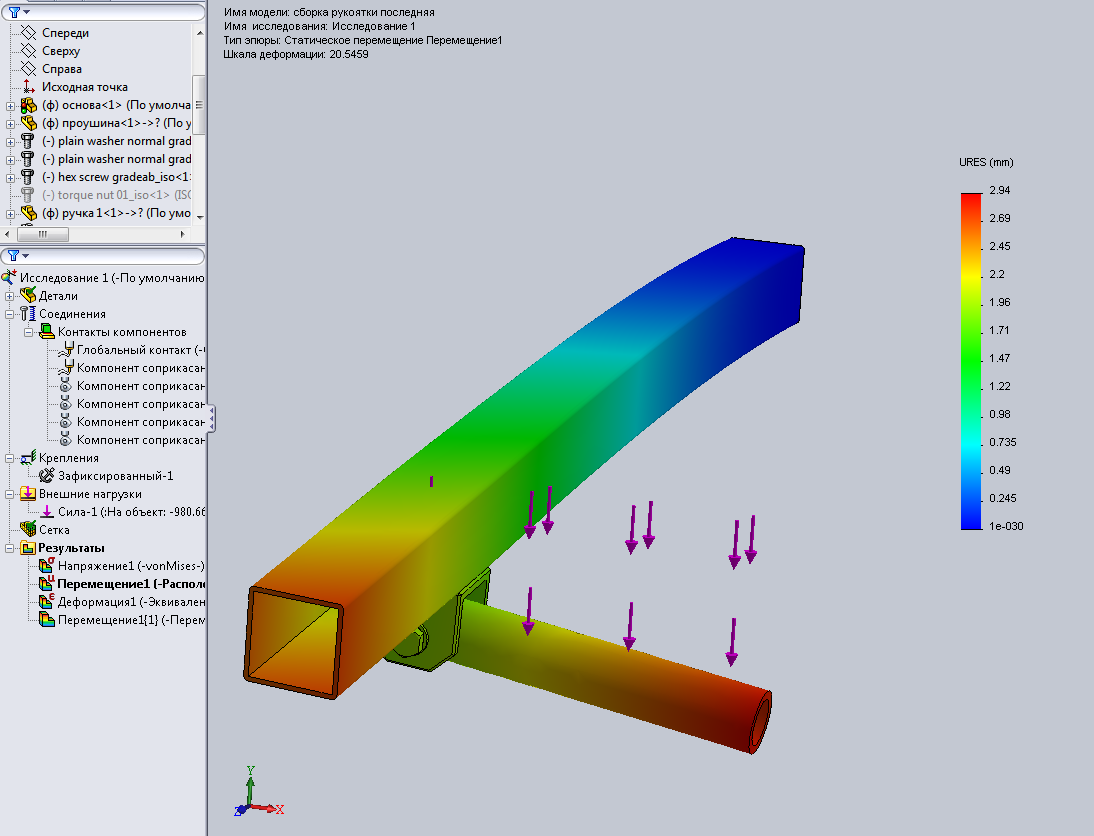
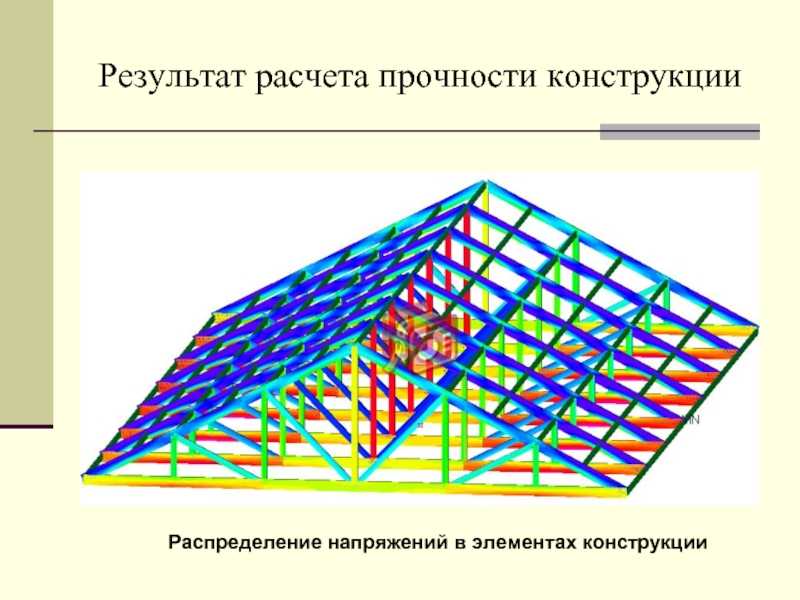
1. Линейный статический расчет:

• распределение напряжений и их составляющих;
• линейные и угловые перемещения;
• деформации;
• внутренние усилия;
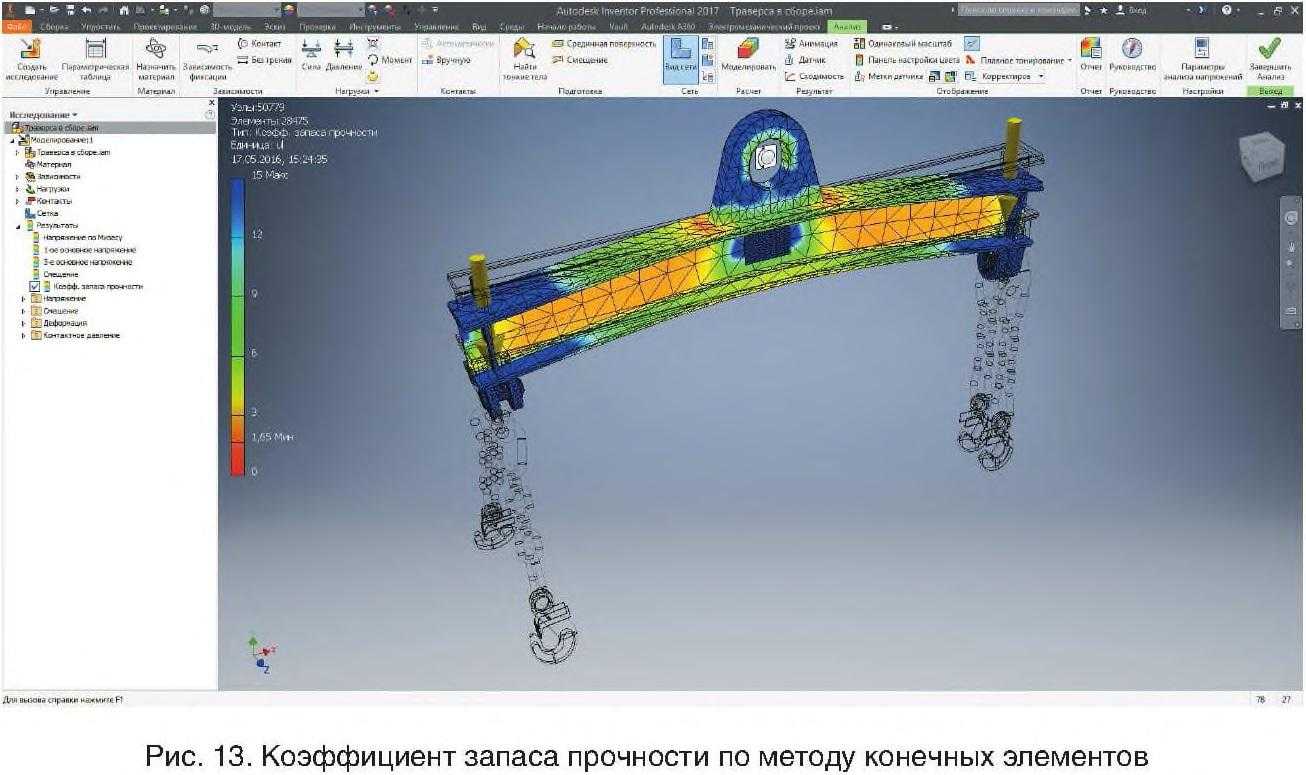
• коэффициенты запаса по текучести и прочности материала.

1. Нелинейный расчет:

• учет геометрической и физической нелинейности;
• контактное взаимодействие;
• моделирование процесса нагрузки и разгрузки.

1. Стационарная и нестационарная теплопроводность:

• специализированные тепловые нагрузки;
• карты распределения температур;
• карты распределения тепловых потоков;
• скорость изменения температуры.

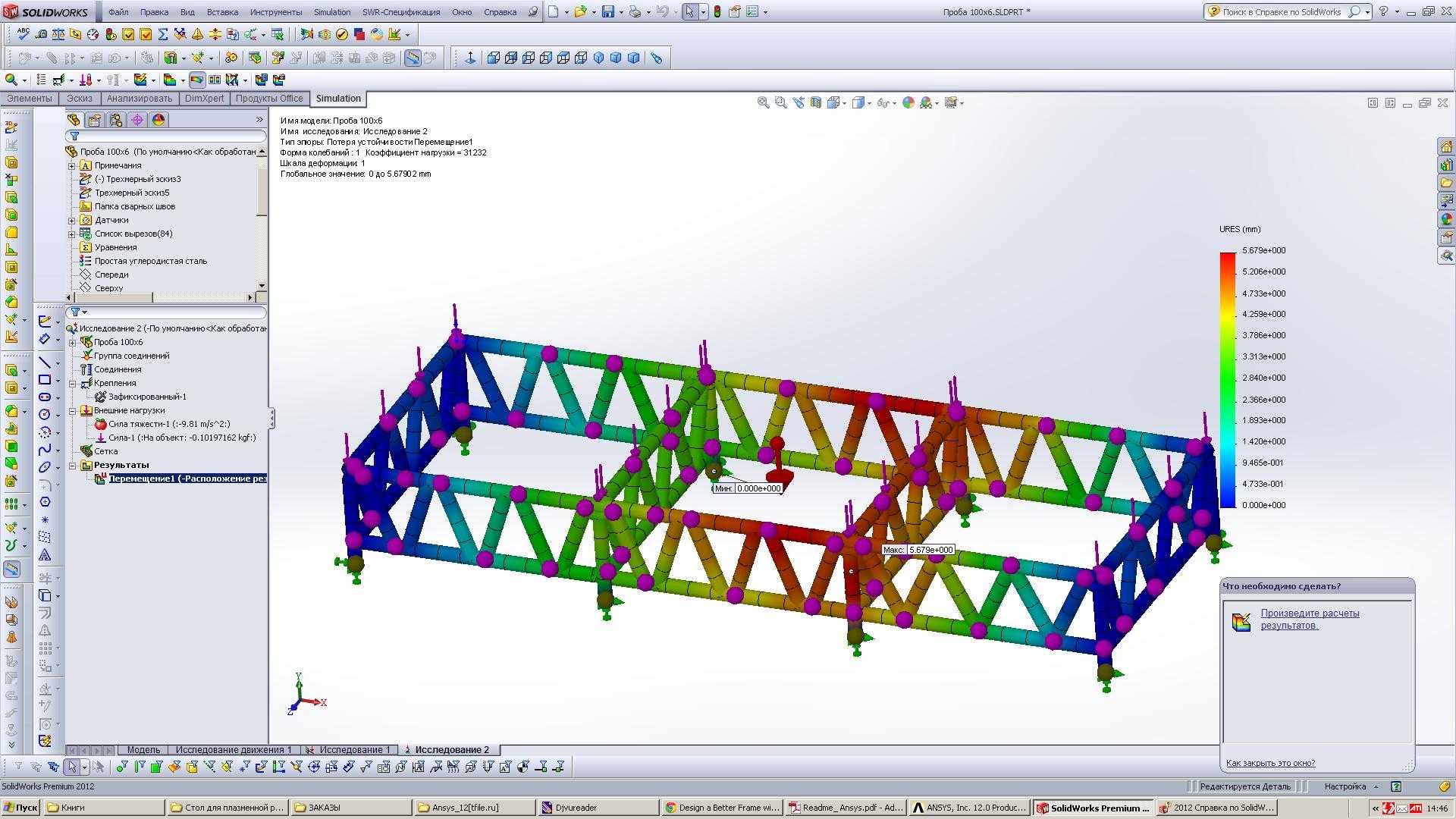
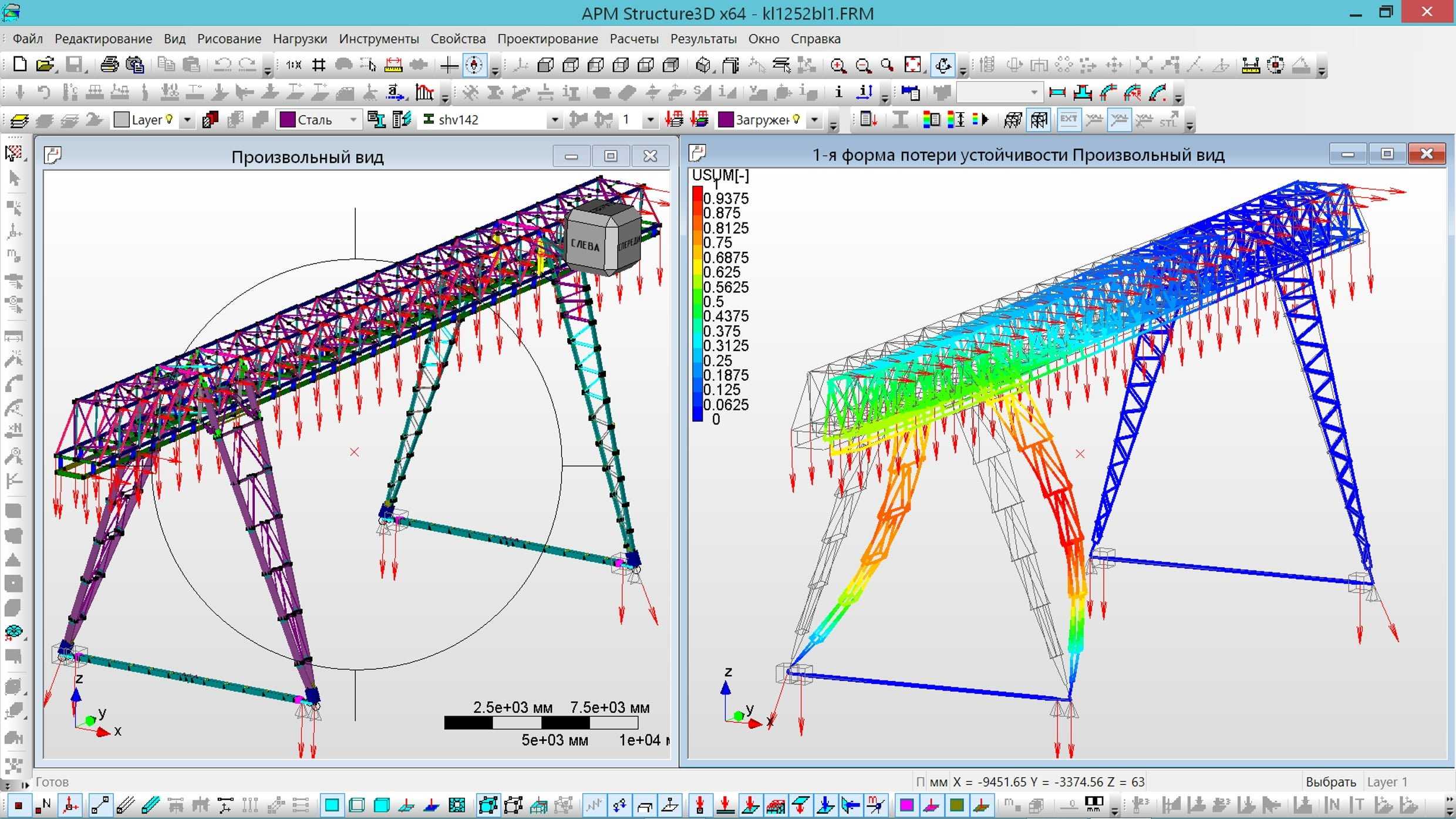
1.  Расчет устойчивости:

• определение коэффициентов запаса;
• построение форм потери устойчивости.

1. Расчет собственных частот:

• определение собственных частот колебаний;
• построение собственных форм.

1. Расчет вынужденных колебаний:

• задание графика изменения вынуждающих усилий;
• анимация карт напряженно-деформированного состояния конструкции;
• проверка отсутствия явлений резонанса.

1. Расчеты соединений в конструкциях:

• резьбовые;
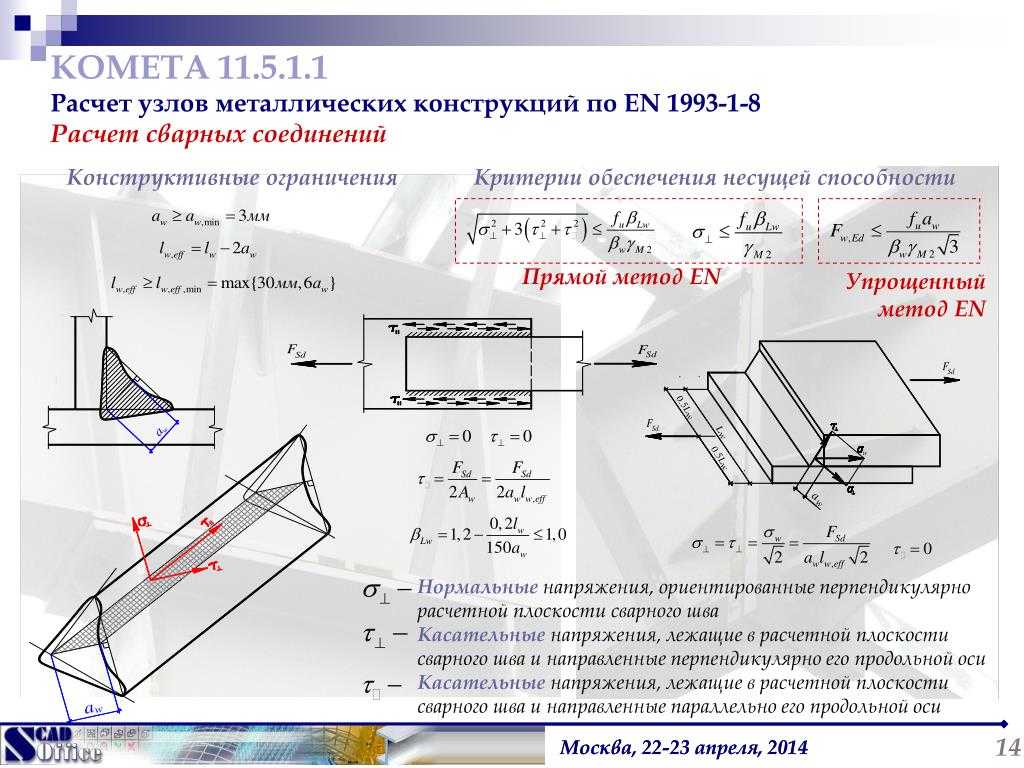
• сварные;
• заклепочные;
• соединения тел вращения.

1. Генерация сеток конечных элементов:

• автоматическая генерация сеток КЭ на поверхностных и твердотельных 3D-моделях;
• постоянный либо переменный (адаптивный) шаг разбиения;
• дополнительные функции предразбиения ребер и поверхностей;
• возможность «ручной» правки созданной КЭ-сетки;
• работа со стержневыми, пластинчатыми и твердотельными КЭ.

Если у вас остались вопросы, связанные с проведением работ по прочностному расчету конструкций, Вы можете обратиться к нам за консультацией и получить подробные ответы на все Ваши вопросы.

Расчет по допускаемым напряжениям

При данной методике материал рассматривается, как некое упругое тело, деформации которого прямо пропорциональны напряжениям.

Методика расчета по допускаемым напряжениям основана на сравнении расчетных напряжений с так называемыми допускаемыми. Допускаемые напряжения определяются как опасные, деленные на коэффициент запаса k, учитывающий все изложенные выше факторы:

= σ_o/k; = т_o/k (319.1.1)

Для пластических материалов опасным напряжением считается предел текучести, за которым следуют значительные пластические деформации:

= σ_т/k₁; = т_т/k₁(319.1.2)

По этим формулам определяются величины допускаемых напряжений при растяжении _р и при кручении тонкостенных стержней _к для сталей различных марок.

Для элементов конструкций или деталей машин, выполненных из хрупких материалов, не имеющих ярко выраженного предела текучести, за опасное напряжение принимается предел прочности:

= σ_в/k₂; = т_в/k₂(319.1.3)

При повторно-переменных нагрузках опасное состояние связано с появлением усталостных трещин, поэтому опасным напряжением считается предел выносливости:

= σ_r/k₃ (319.1.4)

Особенности работы элемента или конструкции могут учитываться введением коэффициентов снижения основных допускаемых напряжений. Ориентировочные значения допускаемых напряжений приведены в таблице 319.1:

Таблица 319.1. Ориентировочные значения допускаемых напряжений

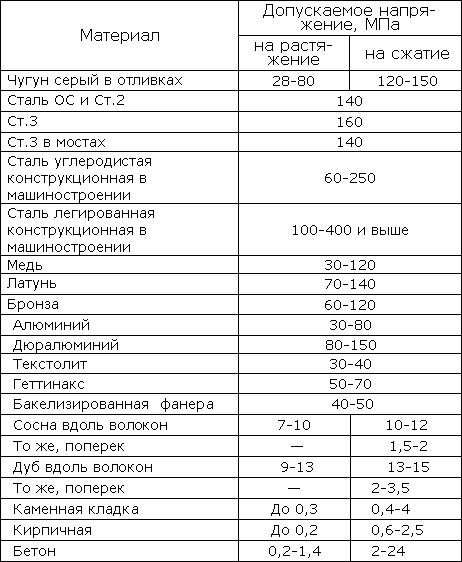
В машиностроении при определении допускаемых напряжений используется один из следующих методов.

1.Дифференцированный — запас прочности определяется как произведение коэффициентов, учитывающих качество материала, точность метода расчета, степень ответственности детали и другие факторы, определяющие условия работы детали.

2.Табличный — допускаемые напряжения принимаются по действующим нормам (по таблицам).

Второй метод менее точен, но более прост, поэтому он нашел более широкое применение в практике проектирования, особенно — в проверочных прочностных расчетах. В данной статье допускаемые напряжения, принимаемые в машиностроении, не приводятся.

В СССР в строительной отрасли методика расчета по допускаемым напряжениям использовалась для расчета железобетонных конструкций до 1938 г., металлических и деревянных конструкций до 1955 г. Тем не менее проектировщики старой закалки и сейчас еще рассчитывают металлические конструкции, пользуясь данной методикой, в частности принимая расчетное сопротивление стали 160 МПа. При расчете конструкций, производящихся в большом количестве, такая методика расчета может приводить к завышенному расходу материалов. А вот в индивидуальном строительстве, при расчете конструкций, выполняемых в количестве от 1 до 10, да еще и с учетом того, что расчет производится непрофессиональным проектировщиком, методика расчета по допускаемым напряжениям, на мой взгляд, должна применяться и сейчас.

Расчет железобетонных конструкций без учета стадии пластических деформаций приводил к повышенному запасу прочности и соответственно завышенному расходу материалов, поэтому для расчета железобетонных конструкций в 30-е годы ХХ столетия была разработана более точная методика расчета железобетонных конструкций: